Tetrahex Bisymmetry Puzzle: Take a full set of seven tetrahexes. Using all the pieces make a figure with horizontal and vertical symmetry (it will also have R2 rotational symmetry). There are 76 different figures (many courtesy of George Sicherman).

See Figures and Solutions

Tetrahex Butterfly Problem A: Take a full set of seven tetrahexes. Select four tetrahex pieces and make two identical copies of a two-piece shape for wings, then use the remaining three pieces to make a symmetrical body. I have found 59 solutions for wing pairs, along with numerous alternate body shapes.  

See Figures and Solutions

Tetrahex Butterfly Problem B: Take a full set of seven tetrahexes. Remove the 1 (or I) piece as a body. Using the remaining six pieces, make two identical copies of a three-piece shape for wings. There are 191 solutions (many courtesy of George Sicherman).

See Figures and Solutions

Tetrahex Butterfly Problem C: Take a full set of seven tetrahexes. Remove the 4 (or Y) piece as a body. Using the remaining six pieces, make two identical copies of a three-piece shape for wings. There are 234 solutions (many courtesy of George Sicherman).

See Figures and Solutions

Tetrahex Butterfly Problem D: Take a full set of seven tetrahexes. Remove the 5 (or U) piece as a body. Using the remaining six pieces, make two identical copies of a three-piece shape for wings. There are 113 solutions (one courtesy of George Sicherman).

See Figures and Solutions

Tetrahex Butterfly Problem E: Take a full set of seven tetrahexes. Remove the 7 (or O) piece as a body. Using the remaining six pieces, make two identical copies of a three-piece shape for wings.

Figures and Solutions coming soon

Tetrahex Propeller Problem: Take a full set of seven tetrahexes. Remove the 3 (or S) piece as a body. Using the remaining six pieces, make two identical copies of a three-piece shape for wings.

See Figures and Solutions

Trihex and Tetrahex Propeller Problem: Take a full set of seven tetrahexes and three trihexes. Remove the 4 (or Y) tetrahex as a body. Using the remaining nine pieces, make three identical copies of a three-piece shape for blades.

Figures and Solutions coming soon

Mono - Tetrahex Propeller Problem: Take a full set of seven tetrahexes, three trihexes, dihex and monohex. Remove the 4 (or Y) tetrahex as a body. Using the remaining eleven pieces, make three identical copies of a 12-unit shape for blades.

Figures and Solutions coming soon

Mono - Pentahex Propeller Problem 1: Take a full set of 22 pentahexes, seven tetrahexes, three trihexes, dihex and monohex. Take 6 pentahexes and make a figure with 6-rotational symmetry. Using the remaining pieces, make 6 identical copies of a 20-unit shape for blades.

Figures and Solutions coming soon

Mono - Pentahex Propeller Problem 2: Take a full set of 22 pentahexes, seven tetrahexes, three trihexes, dihex and monohex. Take 12 pentahexes and make a figure with 6-rotational symmetry. Using the remaining pieces, make 6 identical copies of a 15-unit shape for blades.

Figures and Solutions coming soon

Snowflake Problem 1: Take a full set of 22 pentahexes, seven tetrahexes, three trihexes, dihex and monohex. Take 6 pentahexes and make a figure with full six-fold symmetry. Using the remaining pieces, make 6 identical copies of a 20-unit shape for blades.

See some Figures and Solutions

Snowflake Problem 2: Take a full set of 22 pentahexes, seven tetrahexes, three trihexes, dihex and monohex. Take 12 pentahexes and make a figure with full six-fold symmetry. Using the remaining pieces, make 6 identical copies of a 15-unit shape for blades.

See some Figures and Solutions

Sextuplets Problem: Take a full set of 22 pentahexes, seven tetrahexes, three trihexes, dihex and monohex. Make 6 identical copies of a 25-unit symmetrical shape.

See some Figures and Solutions

Pentahex Dragonfly Problem: Take a full set of 22 pentahexes. Take 2 pentahexes and make a figure with mirror symmetry for the body. Using the remaining pieces, make 4 identical copies of a 20-unit symmetrical shape for wings.

Figures and Solutions coming soon

Tetrahex Portholes Problem: Take a full set of seven tetrahexes. Construct a figure with 6 unit holes which exhibits any form of symmetry. 31 solutions so far

See Figures and Solutions

Tetrahex Tri-rotary Problem: Take a full set of seven tetrahexes. Construct a figure with tri-rotary symmetry. 23 solutions so far

See Figures and Solutions

  See Figures and Solutions

  See Figures and Solutions

  See Some Figures and Solutions

  See Some Figures and Solutions

Penthouses Problem: Take a full set of 12 pentominoes and 5 tetrominoes. Pick 6 pentominoes at random, then make an 11 x 10 rectangle with a hole to fit each of these shapes.

See Figures and Solutions

Polyomino Maze Problems: A series of puzzles based upon the construction of a maze using polyomino pieces.

See Puzzles, Figures and Solutions

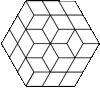Abaroth's Rhombi Problem: Fit 27 edge-coloured rhombi into a hexagon and other shapes.

See Pieces and Solutions

Multihut Problem A: Using the monohut and six dihuts, make a symmetric pattern.

See Figures and Solutions

Abaroth's Cube Problem: Make a cube from the six pieces.

See Pieces and Solution

Monabolic Cube Problem: Make a cube from the six pieces.

See Pieces and Solution