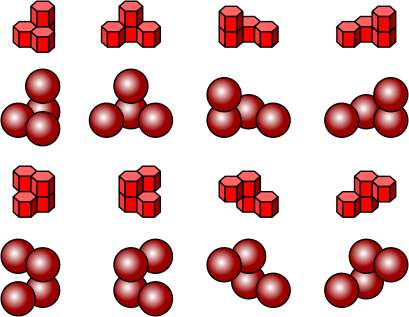
Polyspheres are formed by joining unit spheres in different ways.
There appear to be four different regular & semi-regular lattices into which these pieces can be placed. Only linear pieces can be placed into all four lattices. Actually, there are only three distinct lattices - the pyramidal and tetrahedral lattices are different perspectives of the same arrangement.
| Cubic Lattice | Tetrahedral Lattice | Pyramidal Lattice | Prismatic Lattice |
 |
 |
 |
 |
| This lattice is equivalent to that formed by cubes. | These lattices are identical. Each is equivalent to those formed by rhombic dodecahedra (polyrhons), and truncated octahedra. | This lattice is equivalent to that formed by prismatic hexes | |
 |

 |
 |
|
| Planar pieces are equilvalent to solid polyominoes. Three-dimensional pieces are equivalent to polycubes. | Both solid polyominoes and solid polyhexes can be placed in these lattices. | ||
| The pieces Below are all the planar pieces of orders 1 - 4. On the left are the pieces equivalent to the solid polyhexes, with the solid polyomino equivalents on the right. The linear pieces are common to both sub-sets. |
|||
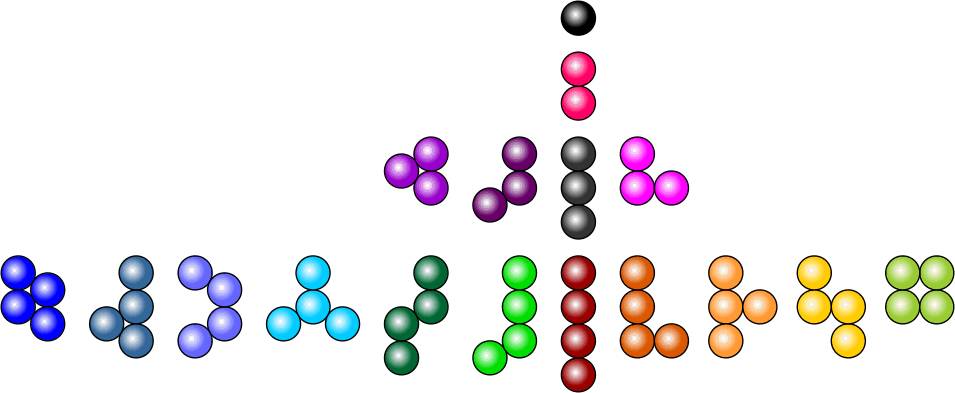 |
|||
|
These pieces can be used to construct
several three-dimensional figures. The colours above are used to
identify the pieces. The level 5 pyramid, the level 5 tetrahedron, the level 6 tetrahedron, the level 4 octahedron, 7 x 4 hipped roof, two pyramidal roofs, the level 5 double tetrahedron, the level 3 hexagonal prism, hexagonal grapes,
|
|||
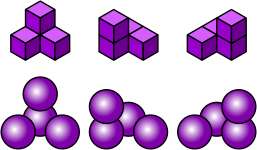
Non-planar pieces |
|||
|
Cubic Lattice Pieces shown in isometric projection, with the equivalent polycubes. |
Pyramidal Lattice Polysphere pieces shown in plan view. Equivalent truncated octahedra shown in isometric projection, with those parts on the second level highlighted. Thanks to Jan de Ruiter for his help in completing these figures.
|
||
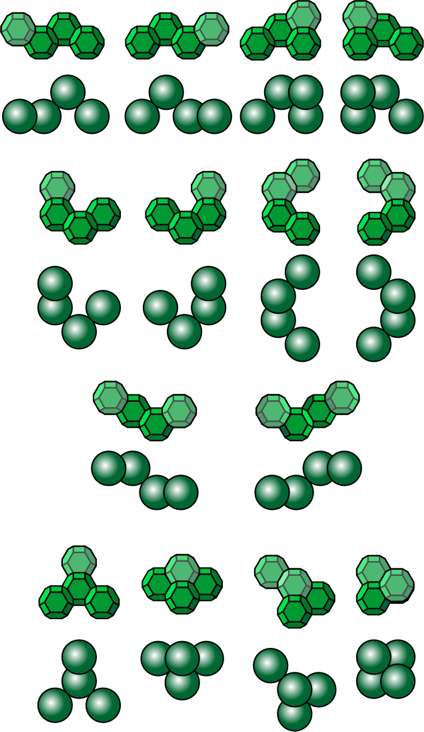
 Prismatic Hexagonal Lattice Pieces shown in isometric projection, with the equivalent prismatic polyhexes.
|
 |
||
| Planar pentaspheres
|
|||
 |
|||
| There are 33 planar pentaspheres, which can exactly fill a level 9 tetrahedron |
|||