Take a full set of 12 pentominoes and 5 tetrominoes. Pick 6 pentominoes at random, then make an 11 x 10 rectangle with a hole to fit each of these shapes. The holes should not touch one another or the edge of the rectangle. There are 924 combinations of pentominoes for the holes. Every combination has many solutions and at least one layout with a unique solution. Many thanks to George Sicherman for his help with this puzzle.
George went on to suggest using six copies of the same pentomino for the holes. We found solutions for F and P, and unique solutions for L, N, T, U, V, W, Y and Z. No solution has been found for I, and it is impossible to place six X holes inside the rectangle.
Odette de Meulemeester has suggested a variation where the 5 tetrominoes are not permitted to touch each other, even at the corners. She added a further version where none of the pentominoes is allowed to touch its own hole shape.
Hover over an image to see a solution.
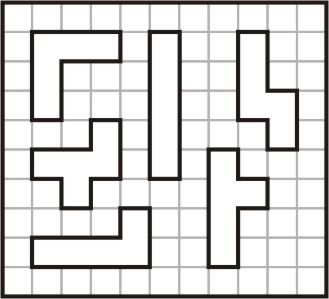 |
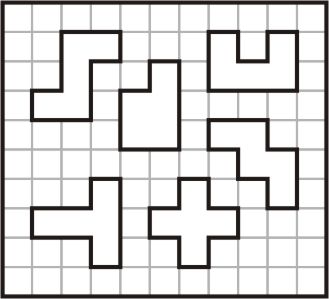 |
| Unique pattern for pieces 1, 2, 3, 4, 5, 6 | Unique pattern for pieces 7, 8, 9, 10, 11, 12 |