I recently found this article on the blog of Alexandre Muņiz: Flexible polyrhombs.
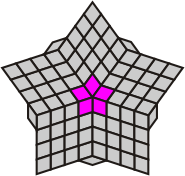
Here is the image he posted of a figure with 5-fold symmetry.
This can be viewed as a construction of pentominoes on 5 angled planes, with the pieces allowed to "flex" across the joints. I coined the name "Flexominoes" for puzzles of this type. Almost immediately, I wondered if I could complete the star shape above using the 5 tetromino pieces, and found that that I could. I also found several more patterns with rotational symmetry before discovering other possibilities using this new topology.
Hover over an image to see a solution.
| Tetra- and pentaflexominoes with 5-fold symmetry | ||
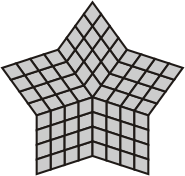 |
||
| The star that led to a whole new galaxy of possibilities | ||
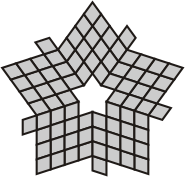 |
 |
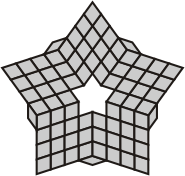 |
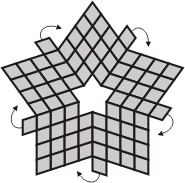
| When I found this solution ... | ... I realised I could "fold" the outer pieces to make ... |
... a more pleasing shape.
|
|
The drawback with these extra
folds, is that it becomes ambiguous as to which of the flexomino shapes make up the "corners". So, I will post both versions for any other patterns which make use of these extra folds, and include an arrow icon in the altered version. |
||
| ||
|
||
| Pentaflexominoes with 3-fold symmetry | ||

|

|

|

|

|

|
| This one is also an impossible object ! | ||
| Pentaflexominoes with 6-fold symmetry | ||

|
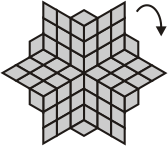
|
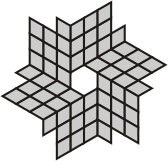
|
| Tetra- and pentaflexominoes with 8-fold symmetry | ||
 |
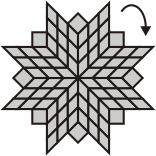 |
 |
| Non-ambiguous version found by Alexandre Muņiz | ||
| Penta -and hexaflexominoes with 5-fold symmetry | ||
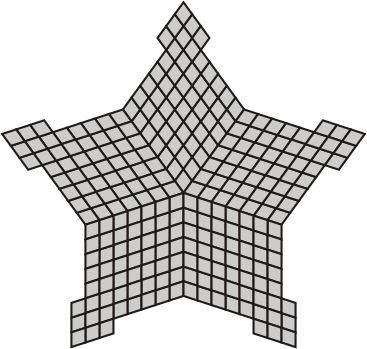 |
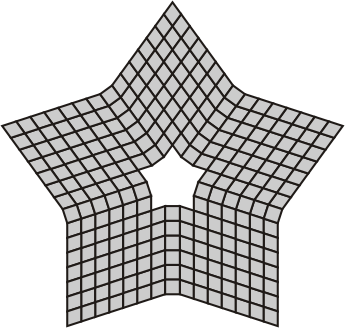 |
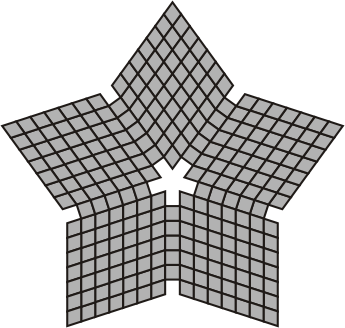 |
| Penta- and hexaflexominoes with 6-fold symmetry | ||
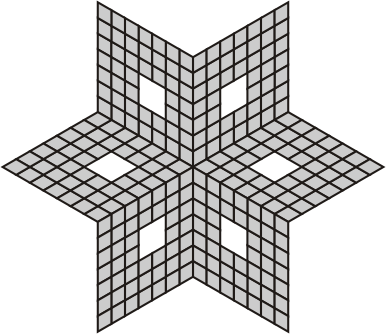 |
||
