These can be viewed as a construction of polyhexes on angled planes, with the pieces allowed to "flex" across the joints. I coined the name "Flexahexes" for puzzles of this type.
Hover over an image to see a solution.
| Flexahexes with 7-fold symmetry | ||
 |
 |
|
| Three sets of tetraflexahexes | Tri-, Tetra- and Pentaflexahexes | |
|
The hexagons here are quite elongated making the polyforms very distorted in some cases. However, this is the only geometry which works where the seven planes contain a central nexus.
|
||
| Tri-, Tetra- and Pentaflexahexes with 7-fold symmetry and no central nexus | ||
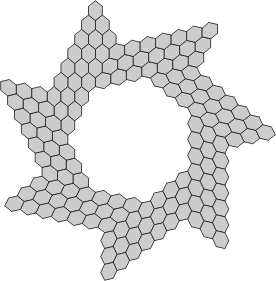 |
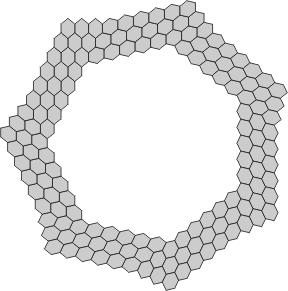 |
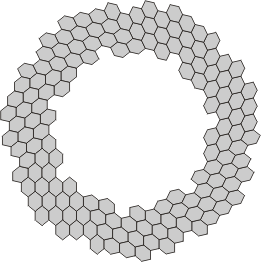 |
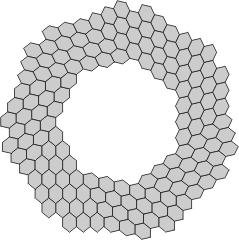 |
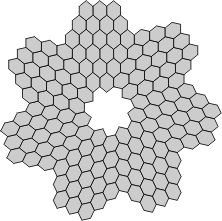 |
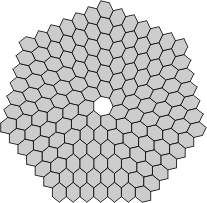 |
| Flexahexes with 5-fold symmetry and no central nexus | ||
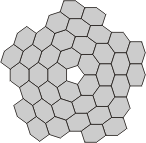 |
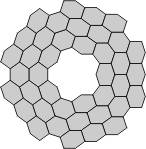 |
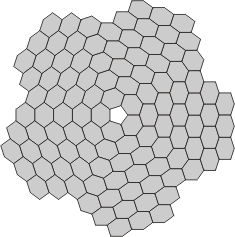 |
| Mono-through-Tetraflexahexes | Mono-through-Tetraflexahexes | Pentaflexahexes |
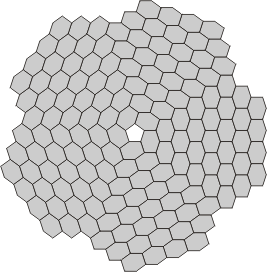 |
 |
|
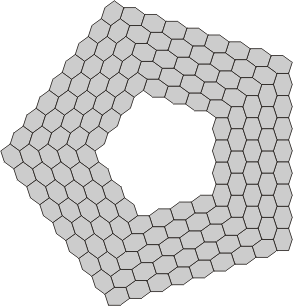
| Mono-through-Pentaflexahexes | Mono-through-Pentaflexahexes | |
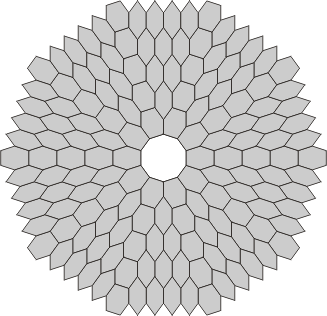
| Flexahexes with 10-fold symmetry and no central nexus | ||
 |
||
| Mono-through-Pentaflexahexes | ||