All images © Abaroth. Permission is given to reproduce for non-profit purposes only.

Home   Historic Sites   Models   Heraldry   Puzzles    Garden   Links

Wikipedia gives the following definition: in recreational mathematics, a polyform is a plane figure constructed by joining together identical basic polygons.

There are many of these strange mathematical creatures out there, and I have been unable to find a comprehensive bestiary so I decided to make one myself. In the process, I discovered that there are infinite numbers of different shapes that can be used, so the list will not be complete. Nevertheless, I hope it provides a useful resource.

The unit is the original polygon which is used to generate the pieces.

The order of a polyform is the number of unit shapes needed to construct it.

Generally, polyforms may be rotated and turned over (reflected). One-sided polyforms comprise sets which contain mirror duplicates of all pieces that are not already symmetric in a mirror. Using these sets, the pieces may only be rotated.

The set of pieces used in any puzzle should be clearly specified. Sets may be: all pieces of a given order; complete sets of several orders; multiple copies of a single tile; or a purely arbitrary selection. For various reasons, people have invented different ways to reduce the number of pieces in a given order or orders. For example, Miroslav Vicher invented the concept of "strip"  polyforms, which comprise those pieces with no branches or clumps.

 

The first family of polyforms live on a square grid.
Name	Description of the unit form	Image
Polyominoes	Square
Polyaboloes	45° right triangle = 1/2 or 1/4 square as shown. The name comes from the diabolo juggling toy which resembles 2 triangles. Also called polytans.
Polyares	Half a square ≡ domino. Named because "are" is half of the word "square". Also called polydominoes, these shapes comprise a subset of polyominoes of double the order. 1 x n-polyare = 1 x 2n-polyomino.
Polydoms	26° 34' right triangle = Half a domino, hence polydom as a name.
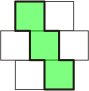
Polyhops & Polybricks	Squares arranged on a modified grid, with alternate rows shifted by 1/2 unit. Named from  hopscotch which uses part of the same grid. The image shows part of the grid with a trihop piece. Polybricks are equivalent to polyhops generated from rectangles, instead of squares. The underlying grid is a modified hexagonal lattice, so pieces can also be constructed from hexagons.
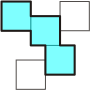
Polyjogs	Squares connected such that every joint is offset by 1/2 unit. The image shows a trijog along with two possible places to add squares. Sets higher than dijogs cannot tile the plane, and contain square spaces, 1/4 the area of the generating unit, which are impossible to fill.
Polynars	The polynars are made from a combined set of polyominoes and polyjogs. They can be thought of as the complete set of pieces which can be formed using the square tetromino as the unit generator.
Polykings or Polyplets	Squares connected edge-to-edge or corner-to-corner. The pieces may cross at cornerwise joints, unlike the rounded or bridged polyominoes.
Polyhuts	Square with a tan joined on the hypotenuse for a "roof". The pieces are a subset of tans of orders which are multiples of 5.
Polysheds	Square with a tan joined on a short side for a "roof". The pieces are a subset of tans of orders which are multiples of 3.
Infinitely many "sets" can be constructed using multiple squares as a unit, but these can also be regarded as a subset of a complete set of a higher order. e.g. polytrominoes are subsets of polyominoes of treble the order. There are also infinitely many unique triangles which can be constructed on the grid.

 

The second family live on a rectangular grid. It is assumed that the rectangles do not possess any special ratio of side lengths which would allow constructions of polyominoes or polyhexes and their families.
Name	Description of the unit form	Image
Polyrects	Rectangle.
Polyograms	Parallelogram.
Polyziums ?	Trapezium.
Polyrhombs	60°, 120° rhombus ≡ diamond. Unlike the polydiamonds, the polyrhombs are confined to the rhombic grid

 

The third family live on a hexagonal grid. This is equivalent to a grid of equilateral triangles, each 1/6th of the hexagon.
Name	Description of the unit form	Image
Polyhexes	Regular hexagon.
Polyhex Variations	Hexagons with modified edges or central holes, which limit the symmetries of the pieces. There are ten different ways to produce sets on the hexagonal grid with restricted symmetries of the generating hexagons.
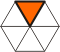
Polyiamonds	Equilateral triangle. Named from the diamond, which looks like the 2nd order piece.
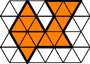
Polymars	The polymars can be thought of as the complete set of pieces which can be formed using the triangular tetriamond as the unit generator. The image shows one of the tetramars.
Polyhes, Polyhalfhexes & Polytriamonds	Three equilateral triangles ≡ triamond.  Named (badly) from "he" which is not half of the word hex. Different grid constraints produce three sets of pieces from this unit shape.
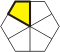
Polykites	1/6th of a hexagon divided by lines from opposing midpoints.
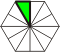
Polydrafters, Polydudes & Extended Polydrafters	30°, 60°, 90° triangle. Named from the drafting tool of the same shape. The polydudes are a subset of polydrafters. Extended polydrafters ignore the grid constraints.
Polypons	30°, 30°, 120° triangle. Named from pons asinorum, Euclid's book on isosceles triangles.
Polyzoids	The trapezoidal shape of a quarter hexagon.
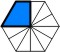Polydiamonds	60°, 120° rhombus ≡ diamond. Pieces are confined to the triangular grid. See also polyrhombs and polycubits.
Polygems	1/3rd of a hexagon divided by lines from opposing midpoints. Named from the shape of the piece, which resembles a brilliant-cut gemstone.
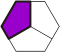Polyflaps	Half a hexagon, bisected by a line from opposing midpoints. Also called Polyflaptiles (from the flap of an envelope).
Polymings	Triangles connected edge-to-edge or corner-to-corner. The pieces may cross at cornerwise joints, unlike the rounded or bridged polyiamonds.
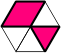Polyhings	Hexagons connected edge-to-edge or corner-to-corner. Shown is a trihing, with one connection of each type.
Polystars	Pieces constructed from a hexagonal body and triangular "rays". The pieces are may be viewed as a restricted subset of polyiamonds.
Polynovae	Like the polystars, but allowing a single triangle to be removed from the hexagonal body.

 

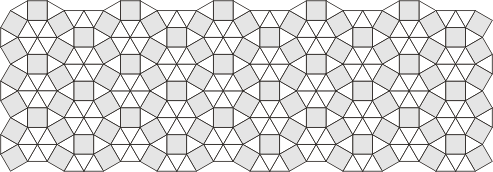
The next family inhabit a grid made of squares and equilateral triangles. Such grids can be made in several ways, so the polyforms that live there are a varied bunch.
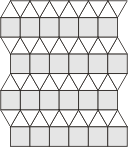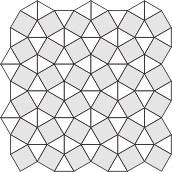A     C B   D
Grids A, B, C contain 2 triangles for each square. So polyforms need to be a multiple or fraction of 2 triangles + 1 square to tile these grids. Grid D contains 14 triangles for every 6 squares - the shaded portion can be viewed as a tiling polyform for this grid. Tiling polyforms could be made from 7 triangles and 3 squares, but any smaller set would need to include a triangle or diamond piece to fill the spaces. Some ambiguity creeps into the definition of sets here: any piece must be composed of square area(s) and triangular area(s). Different arrangements of these areas make different unit pieces - I will call them "siblings" to keep to the family analogy. Whether a set allows siblings or not would need to be made clear. It is also possible to construct pieces on these grids which tile the plane, but not the grids, and I begin with one of these pieces since it has been widely investigated.
Name	Description of the unit form	Image
Polycairos	105°, 90°, 150°, 90°, 105° equilateral pentagon. The shape is formed from an equilateral triangle and two tans. The name derives from paving stones of this shape found in Cairo.
Polygizas	Equilateral triangle + tan attached on a short side. This is the sibling of the polycairo, hence I suggested giza as a name.
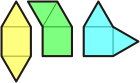
	The 3 siblings formed from a square and 2 triangles.
	The 3 siblings formed from a triangle and a half-square.
	The 3 siblings formed from a 1/2 triangle (drafter) and a 1/4 square (square).
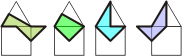
	The 4 siblings formed from a 1/2 triangle (drafter) and a 1/4 square (tan). The second piece in the image has been named a polytwist.
Polyhouses	Square with an iamond "roof". Not to be confused with polyhuts with a tan "roof".
Polywaves	Kite shape formed from an iamond and a tan. One subset are the polywaves, where the pieces are restricted to a distorted square grid, so they resemble polyominoes with wavy edges.
Polyominiamonds	Formed by joining copies of two pieces: a square and an iamond. Note that several of the forms shown above are therefore subsets of polyominiamonds.

 

More polyforms with multiple generators, or polymultiforms.
Name	Description of the unit form	Image
Polyarcs	Formed by joining copies of two pieces: a quarter circle and the remainder of the square from which it was cut.
Polyrounds	Formed by joining copies of two pieces: a circle and the concave square shape formed when circles are arranged in a square grid. These are a subset of polyarcs of orders which are multiples of 4. The image shows the two generating pieces and the diround.
PolyOctagonSquares	Formed by joining copies of two pieces: octagons and squares. The pieces are constrained to the semi-regular octagonal grid. The pieces were first proposed by Livio Zucca.
Rounded or Bridged Polyominoes	Rounded or bridged polyominoes are unit squares which can join edge-to-edge or corner-to corner. Physical pieces can be made in several ways, including using polyarcs or polyoctagonsquares.
Rounded or Bridged Polyiamonds	Rounded or bridged polyiamonds are unit triangles which can join edge-to-edge or corner-to corner.
Polycubits	60°, 120° rhombus ≡ diamond. Pieces are confined to the rhombille grid, with each of the three orientations of the rhombus being regarded as a different piece. See also polyrhombs and polydiamonds.
PolySquareRhombi or Polyskews	Formed by joining copies of two pieces: squares and rhombi. The pieces are constrained to the semi-regular grid as shown. Pieces resemble polyominoes with wavy edges, but there may be up to four different versions of each polyomino. Named Polyskews by Mike Keller in 1994.
Polyores	Formed by joining copies of the two golden isosceles triangles. A) 72°, 72°, 36° triangle and B) 36°, 36°, 108° triangle. The image shows one copy of each triangle forming a larger version of the dark triangle.

 

The next group are not a family. However, none of them tile the plane without leaving spaces.
Name	Description of the unit form	Image
Polypents	Regular pentagon
Polyhepts	Regular heptagon
Polyocts	Regular octagon
Polypentagrams	Regular pentagram
Polypennies	Circle. The pieces are distinguished by unique topology, rather than graphically. In other words, each penny can be regarded as if magnetically connected to up to six neighbours. The pieces are free to assume any shape, so long as no connections are broken, or new ones created.
Polysticks	Lines of unit length joining adjacent points on a square grid. The image shows three tetrasticks.
Polytwigs	Lines of unit length joining adjacent points on a hexagonal grid.
Polytrigs	Lines of unit length joining adjacent points on a triangular grid.

 

Other polyforms.
Name	Description of the unit form	Image
Hinged Polyforms	Shapes connected at the vertices, and allowed to pivot if geometry allows. The image shows two copies of the same hinged tetromino to illustrate. Certain pieces have limited or no flexibility.
Flexominoes	Distortion of standard polyominoes into different rhombi. The standard sets of polyominoes are used, but the pieces are regarded as pieces of paper which may be folded along the gridlines. This allows solutions with symmetries other than those of the square grid. The image shows a 5-fold symmetric pattern of tetra- and pentaflexominoes.
Flexahexes	The same trick as above, applied to sets of polyhexes. The image shows a 5-fold symmetric pattern of the mono-through-tetraflexahexes.
Constellations	A slightly more abstract version of polyform, constellations are formed from points and connecting lines of different geometry & topology.