There are 17 different symmetries which can be used to make tessellations and wallpaper. There are many pages with technical information about the 17 wallpaper groups, but most are difficult to understand. Here is one that explains them in a much simpler way than most - World of Mathematics.
I set myself the problem of finding how many polyforms would be needed to create all of the 17 patterns, and would you believe the answer is two - a square and a drafter (30, 60, 90 triangle). Actually, it is possible to split each square diagonally into four tans (45, 45, 90 triangles) and reduce the vertex count of the shapes by one.
| Group | Image | Symmetries |
| P1 |
 |
Translations only |
| P2 |
 |
180° Rotation |
| PM |
 |
Mirror |
| PG |
 |
Glide Reflection |
| PMM |
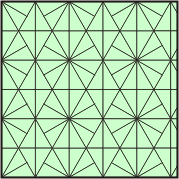 |
Two mirrors set 90° apart. |
| PMG |
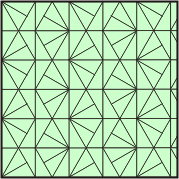 |
Reflection and 180° Rotation |
| PGG |
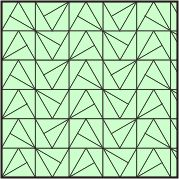 |
Glide Reflections and 180° Rotation |
| CM |
 |
Mirror |
| CMM |
 |
Two mirrors set 90° apart. |
| P4 |
 |
90° Rotation |
| P4M |
 |
90° Rotation and four mirrors set 45° apart |
| P4G |
 |
90° Rotation and two mirrors set 90° apart |
| P3 |
 |
120° Rotation |
| P3M1 |
 |
120° Rotation and mirror. |
| P31M |
 |
120° Rotation and mirror. |
| P6M |
 |
60° Rotation and 6 mirrors set 60° apart. |
| P6 |
 |
60° Rotation |
I expect mirrors and rotations are familiar terms for symmetric patterns, but what about translations and glide reflections? To say that an object has symmetry means that you can do something to the object and it looks exactly the same as it did before. Yet translations mean the object has moved, so how does that apply to symmetry? The key here is that we are talking about repeated patterns which can extend to infinity. Imagine looking at a black square of an infinite chequerboard pattern. Now close your eyes. The board moves so that a different black square occupies the precise position of the first one. Now open your eyes. Everything appears exactly as it did before, but the whole pattern has been moved or translated. A glide reflection works in exactly the same manner, but this time the board is moved and reflected whilst your eyes are closed.