All images © Abaroth. Permission is given to reproduce for non-profit purposes only.

Home   Historic Sites   Models   Heraldry   Puzzles   Garden   Links

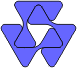
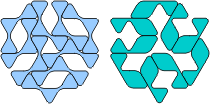
Rounded Triamond Puzzles

These puzzles use the eleven rounded or bridged triamonds. The pieces cover an area of 33 unit triangles. Patterns are considered symmetric regardless of the position of the bridges joining the triangles.

 

Geometric Forms

Use all the pieces to make a symmetric pattern. Here are examples for the different types of symmetry.
Type of Symmetry
Ternary and Reflected	Trirotary	Reflected

Butterflies

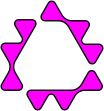
Butterfly puzzles have a single symmetric piece removed as a body, with the remaining pieces used to make two identical wings. Here is an example of each type.

Oddities

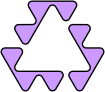
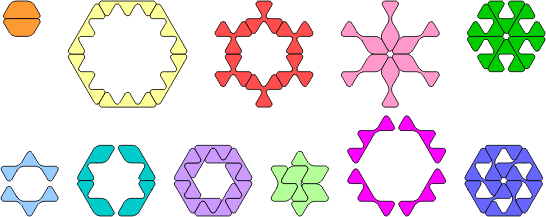
An oddity is a figure with binary symmetry formed by an odd number of copies of a polyform. You can find more about Polyform Oddities  at George Sicherman's Polyform Curiosities website. Here are the minimal oddities for the rounded triamonds.

Compatibilities

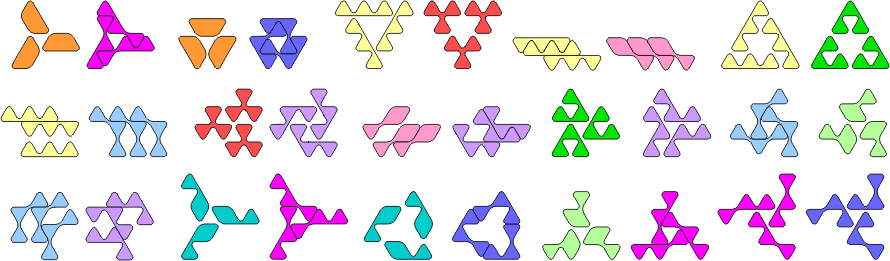
Polyforms are compatible if there is a shape that can be tiled by each. You can find more about Polyform Compatibility at George Sicherman's Polyform Curiosities website. Here are minimal known compatibilities for the rounded triamonds, several of which were solved or improved by George.

	*	2	6	2	2	?	2	2	2	3	3
	2	*	3	3	3	3	2	2	2	2	2
	6	3	*	R	R	?	2	2	3	2	6
	2	3	R	*	6	2	2	2	3	2	2
	2	3	R	6	*	?	2	2	3	2	2
	?	3	?	2	?	*	9	3	3	2	2
	2	2	2	2	2	9	*	2	2	3	3
	2	2	2	2	2	3	2	*	2	3	2
	2	2	3	3	3	3	2	2	*	2	2
	3	2	2	2	2	2	3	3	2	*	3
	3	2	6	2	2	2	3	2	2	3	*

2 Tiles

3 Tiles

6 Tiles

9 Tiles

Reëntrant Solutions

Baiocchi Figures

Baiocchi figures were first proposed by Claudio Baiocchi in 2008. A Baiocchi figure is formed by joining copies of a single polyform and has full symmetry - in this case sextarotary with reflection. You can find more about Baiocchi Figures at George Sicherman's Polyform Curiosities website. Here are minimal known Baiocchi Figures for the rounded triamonds.