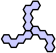
Symmetries of Polyhexes
There are ten possible symmetries using polyhex pieces. I use the convention that the pieces are always shown with a flat side at the top and bottom, and points at the sides. The terms "Horizontal" and "Vertical" apply to patterns using this convention. No. Type of Symmetry
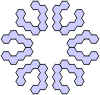
Example Notes 1 Full The maximum number of symmetries for the polyhexes is 12. There are six rotations and six reflections. A solution must contain n x 6 or n x 6 + 1 unit hexes.
2 Sextarotary A pattern with six rotations. A solution must contain n x 6 or n x 6 + 1 unit hexes.
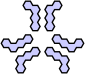
3 Ternary & Horizontal A pattern with three rotations and three reflections, with the mirrors through the faces of the central hex. A solution must contain n x 3 or n x 3 + 1 unit hexes.
4 Ternary & Vertical A pattern with three rotations and three reflections, with the mirrors through the points of the central hex. A solution must contain n x 3 or n x 3 + 1 unit hexes.
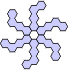
5 Trirotary A pattern with three rotations. A solution must contain n x 3 or n x 3 + 1 unit hexes.
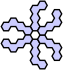
6 Double Bilateral A pattern with two perpendicular reflections. A solution may contain any number of unit hexes.
7 Birotary A pattern with two rotations. A solution may contain any number of unit hexes.
8 Horizontal A pattern with one reflection, with the mirror through the faces of the central column. A solution may contain any number of unit hexes.
9 Vertical A pattern with one reflection, with the mirror through the points of the central row. A solution may contain any number of unit hexes.
10 None A pattern with no symmetries. A solution may contain any number of unit hexes.
Parity and Polyhexes
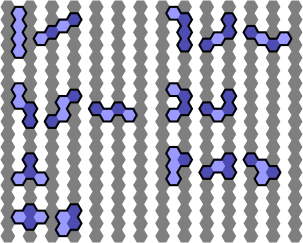
Checking parity on a square grid is matter of colouring the pieces and the field with a chequerboard pattern. Any piece can have the same number of dark and light squares called "even parity", or different numbers of each, which is "odd parity". The parity is unchanged by rotations or reflections. Parity on the hexagonal grid is more complex. To begin, alternate columns of the field are shaded and the tetrahex pieces are placed on this grid in different orientations. Horizontal and vertical reflections of the pieces are possible, but they have no effect on the parity for this grid, however rotations of the pieces can change their parity, as shown.
Grid Pieces 1. Always even parity. Either all one colour, or alternate dark/light hexes. 2. Can exhibit odd or even parity. 3. Always even parity 4. Always even parity 5. Can exhibit odd or even parity. 6. Can exhibit odd or even parity. 7. Always even parity