Rounded or Bridged Polyominoes can be regarded as unit squares joined edge-to-edge or corner-to corner. The cornerwise joints are regarded as being solid - unlike those of polykings, which may cross at these points. Physical pieces can be constructed in several ways, which include using polyarcs, bridged circles, polyoctagonsquares, joined circles or rounded squares.
Rounded Monomino - 1 (1 tile)
|
|
Rounded Dominos - 2 (4 tiles)
|
|
 |
|||
| 1 | 2 |
Rounded Trominos - 5 (15 tiles)
|
|
 |
 |
 |
 |
| 1 | 2 | 3 | 4 | 5 |
Rounded Tetrominos - 22 (88 tiles)
|
|
 |
 |
 |
 |
| 1 | 2 | 3 | 4 | 5 |
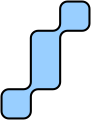
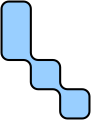
| I | L | T | N | O |
 |
 |
 |
 |
 |
| 6 | 7 | 8 | 9 | 10 |
| J | S | C | V | K |
 |
 |
 |
 |
 |
| 11 | 12 | 13 | 14 | 15 |
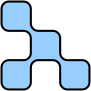
| Y | Z | P | R | Q |
 |
 |
 |
 |
 |
| 16 | 17 | 18 | 19 | 20 |
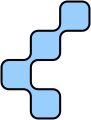
| F | G | O | T | N |
 |
 |
|||
| 21 | 22 | |||
| L | I |
For higher orders of polyominoes, the number of pieces is as follows:
Rounded Pentominos - 99
Rounded Hexominos - 580
Rounded Heptominos - 3557
The pieces diverge from the polykings above the fourth order, when some pieces may be joined by bridges in different positions. Shown below are the rounded pentominos with bridge variations.

Puzzles using Rounded Polyominos
