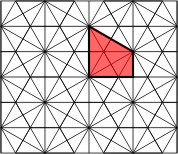
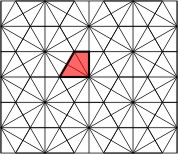
Polyzoids are formed from one quarter of a hexagon. They form a subset of the polydrafters of three times the order. The pieces are confined to a polydrafter grid. If the pieces are allowed to break this first grid, then we can create the extended polyzoids, which lie within the grid in a different way as shown below.
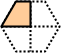
Monozoid - 1 (1 tile)
 |
Dizoids - 7 (14 tiles) + Extended dizoids - 5 (10 tiles)
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
| 6 | 7 | 8* | 9* | 10* |
|
|
|
|||
| 11* | 12* |
Trizoids - 24 (72 tiles) + Extended trizoids - 85 (255 tiles, not pictured)
|
|
|
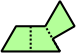 |
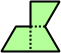 |
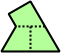 |
| 1 | 2 | 3 | 4 | 5 |
 |
 |
|
|
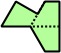 |
| 6 | 7 | 8 | 9 | 10 |
|
|
|
|
 |
|
| 11 | 12 | 13 | 14 | 15 |
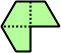 |
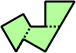 |
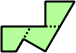 |
 |
 |
| 16 | 17 | 18 | 19 | 20 |
 |
|
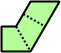 |
 |
|
| 21 | 22 | 23 | 24 |
For higher orders of polyzoids, the number of pieces is as follows:
Tetrazoids - 147 + Extended tetrazoids -1,310
Pentazoids - 839 + Extended pentazoids - 18,256
Hexazoids - 5,461 + Extended hexazoids - ?
Heptazoids - ? + Extended heptazoids - ?