Polyhes are formed from three equilateral triangles, or half a hexagon cut corner-to-corner. They form a subset of the polyiamonds of three times the order. The pieces are confined to the hexagonal grid, such that each grid cell can contain only one monohe. Keeping to the grid, but allowing a cell to contain a complete hexagon, we get a set named polyhalfhexes. Removing the grid restrictions completely, we arrive at a complete set of polytriamonds.
Monohe / Monohalfhex / Monotriamond - 1 (1 tile)
|
|
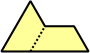
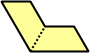
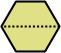
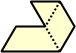
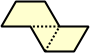
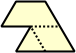
Dihes - 4 (8 tiles) + Dihalfhexes - 5 (10 tiles) + Ditriamonds - 9 (18 tiles)
|
|
 |
 |
 |
 |
| 1 | 2 | 3 | 4 | 5 |
 |
 |
 |
 |
|
| 6 | 7 | 8 | 9 |
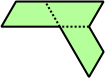
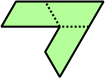
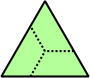
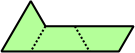
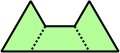
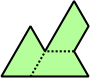
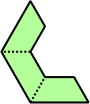
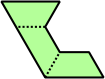
Trihes - 13 (39 tiles) + Trihalfhexes - 15 (45 tiles) + Tritriamonds (not pictured) - 94 (282 tiles)
|
|
 |
 |
 |
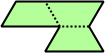 |
| 1 | 2 | 3 | 4 | 5 |
 |
 |
 |
 |
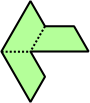 |
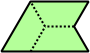
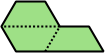
| 6 | 7 | 8 | 9 | 10 |
 |
 |
 |
 |
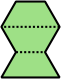 |
| 11 | 12 | 13 | 14 | 15 |
|
Polyhes |
Polyhalfhexes |
Polytriamonds |
|
Tetrahes - 60 |
Tetrahalfhexes - 82 |
Tetratriamonds - 1552 |
|
Pentahes - 276 |
Pentahalfhexes - 429 |
Pentatriamonds - 27285 |
|
Hexahes - 1416 |
||
|
Heptahes - 7201 |
||
|
Octahes - 37972 |
|
|
|
|
|
|
|
|
|
|